ALTIN ORAN VE FİBONACCİ DİZİSİ

Çiğdem Sarıgül 17 Haziran 2015

1 23.683 3 dakika okuma süresi

Altın oran, Fi (phi) sayısı olarak bilinir. Neticede matematiksel bir kavramdır ve değeri de 1,618 dir.

Fibonacci sayıları ve altın oran matematiğin en ilgi çekici konuları arasındadır. Fibonacci dizisinin mucidi Leonardo Fibonacci 13. yüzyılda yaşamış bir İtalyan matematikçisiydi.

FİBONACCİ DİZİSİ: 1,1,2,3,5,8,13,21,34,55,89,144….

Bu diziye baktığımız zaman onun basit bir kurala dayanarak oluşturulduğunu görebiliriz. Bu kuralı sözcüklerle ifade edersek; her sayı (ilk ikisi dışında) kendisinden önce gelen iki sayının toplamından oluşmuştur. Dizinin ilerleyen sayılarında alınan bir terimin bir önceki terime oranı altın orana yakınlaşmaktadır.

ALTIN ORANIN GÖRÜLDÜĞÜ VE KULLANILDIĞI YERLER:

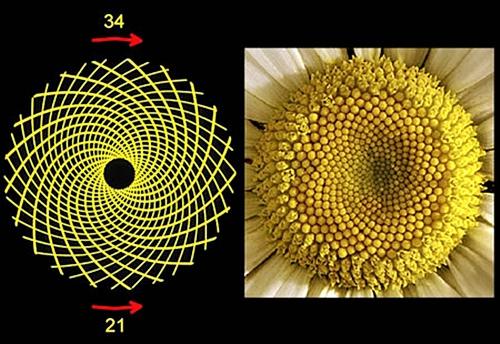
1) Ayçiçeği: Ayçiçeğinin merkezinden dışarıya doğru sağdan sola ve soldan sağa doğru tane sayılarının birbirine oranı, altın oranı verir.

2) Papatya: Papatya çiçeğinde de ayçiçeğinde olduğu gibi bir altın oran mevcuttur.

3) Mısır Piramitleri: Her bir piramidin tabanının yüksekliğine oranı yine altın oranı veriyor.

4) Leonardo da Vinci: Bilindiği gibi Leonardo da Vinci Rönesans devri ünlü ressamlarındandır. Şimdi bu ünlü ressamın çizmiş olduğu tabloları inceleyelim.

Mona Lisa: Bu tablonun boyunun enine oranı altın oranı verir.

Aziz Jerome: Yine tablonun boyunun enine oranı bize altın oranı verir.

Cool Picasso: Picasso da Leonardo da Vinci gibi ünlü bir ressamdır ve resimlerinde bu oranı kullanmıştır.

5) Çam Kozalağı: Çam kozalağındaki taneler kozalağın altındaki sabit bir noktadan kozalağın tepesindeki başka bir sabit noktaya doğru spiraller (eğriler) oluşturarak çıkarlar. İşte bu eğrinin eğrilik açısı altın orandır.

6) Deniz Kabuğu: Deniz kabuğunun yapısı incelendiğinde bir eğrilik tespit edilmiş ve bu eğriliğin tanjantının altın oran olduğu görülmüştür.

7) Tütün: Tütün Bitkisinin yapraklarının dizilişinde bir eğrilik söz konusudur. Bu eğriliğin tanjantı altın orandır. Aynı özellik eğrelti otunda da vardır.

8) Elektrik Devresi: Altın Oran sadece Matematik ve kâinatta değil, Fizik’te de kullanılıyor. Verilen n tane dirençten maximum verim elde etmek için bir paralel bağlama yapılması gerekir. Bu durumda Eşdeğer Direnç, yani Reş = altın oran olur.

9) Salyangoz: Salyangozun Kabuğu bir düzleme aktarılırsa, bu düzlem bir dikdörtgen oluşturur (ki biz bu dikdörtgene altın dikdörtgen diyoruz) İşte bu dikdörtgenin boyunun enine oranı yine altın oranı verir.

10) Mimar Sinan: Mimar Sinan’ın da birçok eserinde bu altın oran görülmektedir. Mesela Süleymaniye ve Selimiye Camileri’nin minarelerinde bu oran kullanılmıştır.

11) Arı Kovanları: Arı kovanlarında yaşayan dişi arıların sayısının erkek arıların sayısına bölündüğünde hep aynı sayı elde edilir. Yani 1.618

12) Sanatta: Michelangelo, Albrecht Dürer, Da Vinci ve diğerlerinin sanat eserlerinde, Altın Orana bilinçli ve dikkatli bir bağlılık söz konusudur. Beethoven in Beşinci Senfonisinde, Bartok’un, Debussy’nin ve Shubert’in eserlerinde de gözükür. Stradivarius’ un bile ünlü kemanlarındaki F deliklerinin yerlerini belirlemekte altın oranı kullandığı bilinmektedir.

İNSAN VÜCUDUNDA ALTIN ORAN

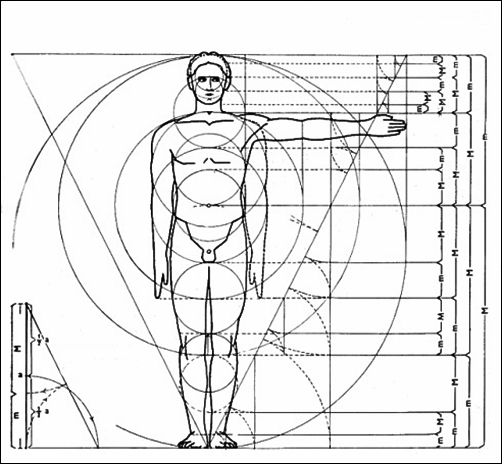
İnsan gözünün altın orana bu kadar yakın olmasının, estetik açıdan sürekli olarak altın orana uygun şekil ve yapıları tercih etmesinin bir nedenini, yaşadığı çevre olan doğada hemen her an altın oranla karşı karşıya olmasının yanı sıra, kendi vücudunun hemen her noktasında altın orana sahip olmasında arayabiliriz. Aşağıda oranlarda insanında ne kadar altın oran örneği olduğunu göreceksiniz:

Tam Boy / Bacak boyu

Beden Boyu / Kol altı beden boyu

Parmak ucu – Omuz boyu / Parmak ucu – Dirsek boyu

Göbek – Omuz boyu / Göbek – Bel boyu

Kollar: İnsan vücudunun bir parçası olan kolları dirsek iki bölüme ayırır. Büyük (üst) bölüm ve küçük (alt) bölüm olarak. Kolumuzun üst bölümünün alt bölüme oranı altın oranı vereceği gibi, kolumuzun tamamının üst bölüme oranı yine altın oranı verir.

Parmaklar: Ellerimizdeki parmaklarla altın oranın ne alakası var diyebilirsiniz. İşte size alaka… Parmaklarınızın üst boğumunun alt boğuma oranı altın oranı vereceği gibi, parmağınızın tamamının üst boğuma oranı yine altın oranı verir.

İNSAN YÜZÜNDE ALTIN ORAN

İdeal ölçülere sahip bir insan yüzünde de sayısız altın oran örnekleri görmek mümkündür:

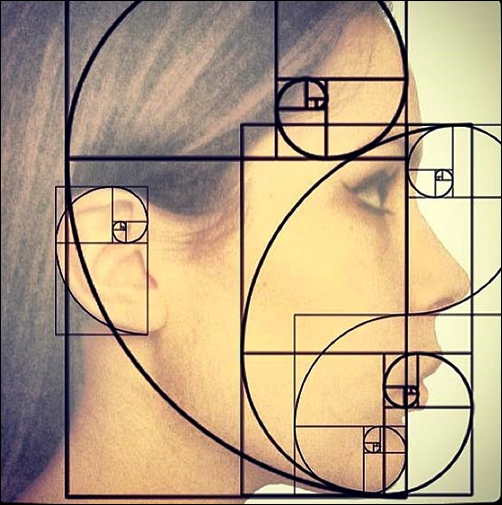Yüz yüksekliği / Yüz genişliği